定积分的计算一般思路与步骤(不定积分计算思路从step3开始):
Step1:分析积分区间是否关于原点对称,即为[-a,a],如果是,则考虑被积函数的整体或者经过加减拆项后的部分是否具有奇偶性,如果有,则考虑使用“偶倍奇零”性质简化定积分计算.
Step2:考虑被积函数是否具有周期性,如果是周期函数,考虑积分区间的长度是否为周期的整数倍,如果是,则利用周期函数的定积分在任一周期长度的区间上的定积分相等的结论简化积分计算.
Step3:考察被积函数是否可以转换为“反对幂指三”五类基本函数中两个类型函数的乘积,或者是否包含有正整数n参数,或者包含有抽象函数的导数乘项,如果是,可考虑使用定积分的分部积分法计算定积分.
Step4:考察被积函数是否包含有特定结构的函数,比如根号下有平方和、或者平方差(或者可以转换为两项的平和或差的结构),是否有一次根式,对于有理式是否分母次数比分子次数高2次以上;是否包含有指数函数或对数函数,对于具有这样结构的积分,考虑使用三角代换、根式代换、倒代换或指数、对数代换等;换元的函数一般选取严格单调函数;与不定积分不同的是,在变量换元后,定积分的上下限必须转换为新的积分变量的范围,依据为:上限对上限、下限对下限;并且换元后直接计算出关于新变量的定积分即为最终结果,不再需要逆变换换元!
【注1】不管是分部积分法还是换元法(第一类换元法),一般是将被积函数分解为两个函数的乘积,然后考察简单函数的原函数,一般思路为(假设函数h(x)为简单函数):

【注2】对于两个函数的乘积,在寻找h(x)的原函数的过程中,注意观察可能的原函数结构与余下函数的关系,通过构造函数(加、减、乘、除函数项弥补需求)得到函数的原函数。
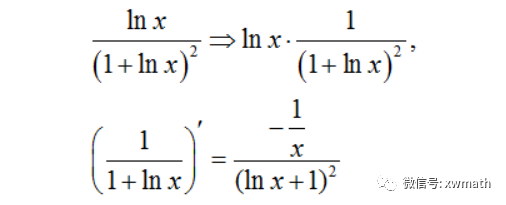
考虑到分式求导公式,并结合导数结果,容易发现,如果求导的函数多一个分子x,则正好符合要求,所以就有
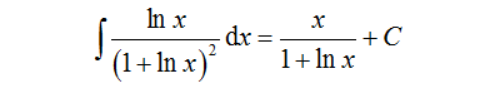
【注3】考虑简单函数的导数来寻找余下函数的关系来构造合适的换元方式与计算方法。
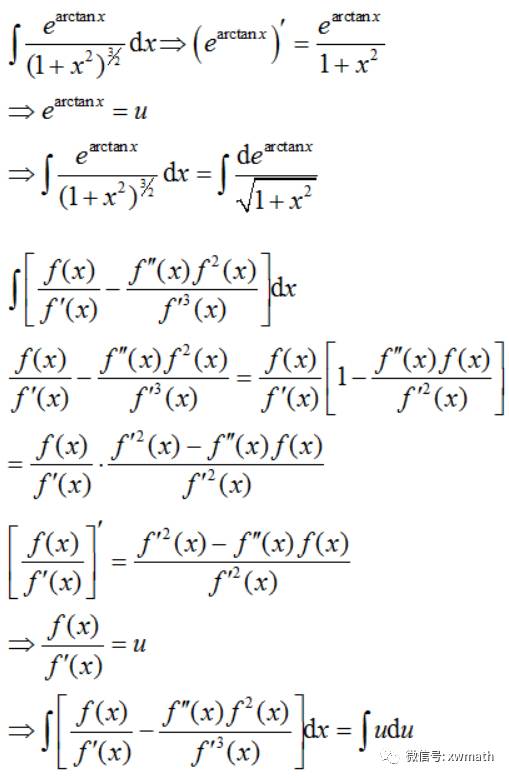
【注4】记得三角代换的三个三角形用来逆代换三角函数表达式.
例1:设
求{an} (n=1,2,…)所有项的和.
【思路一】
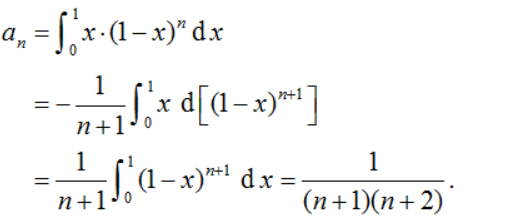
【思路二】
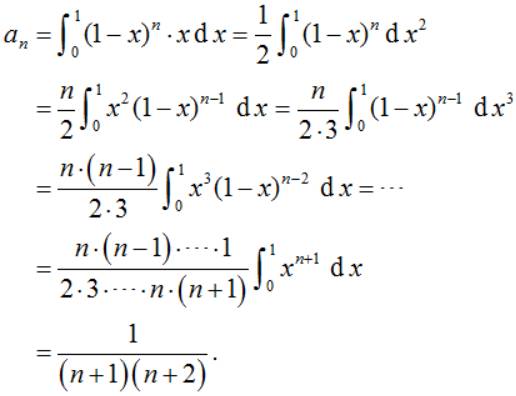
【思路三】令t=1-x,则
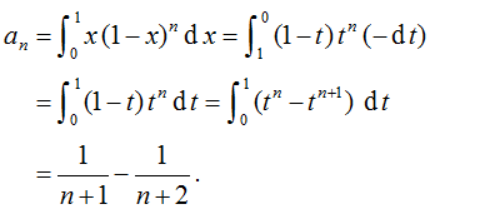
从而
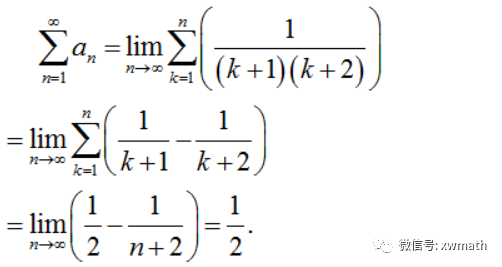
例2:计算不定积分
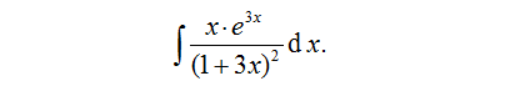
【思路】使用以上分解函数的方法,借助分部积分问题越来越复杂,由于问题中包含有指数函数,又不能直接换成“反对幂指三”的结构,所以考虑对指数函数换元。
【解】:令e3x=t,于是有3x=lnt,x=lnt/3,且dx=1/(3t)dt,于是有
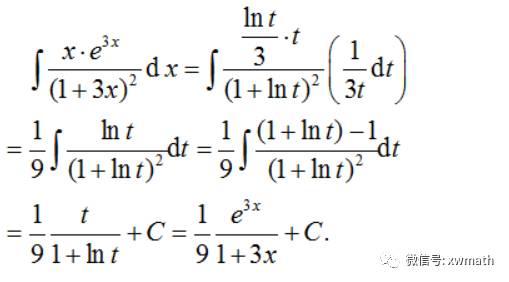
更多高等数学内容与学习交流可关注微信公众号:考研实验数学(ID: xwmath),我们的大学数学公共基础课程分享交流平台!
版权声明
本文仅代表作者观点,不代表百度立场。
本文系作者授权百度百家发表,未经许可,不得转载。









发表评论